Motivation vs choice
Using constrained optimisation to distinguish between interventions aimed at changing motivation and those aimed at influencing choices
An important element of the integrated approach is that it combines psychological behaviour change models, which focus on motivation, with economic ones, which focus on choice. This article explores how the framework of ‘constrained optimisation’ allows one to analyse the difference between interventions that affect choice and those that affect motivation and makes predictions about how they will affect an individual’s happiness.
Setting up the model
Constrained optimisation rests on two central assumptions. The first is that we have limited resources in terms of money (and time and effort). This is where the ‘constrained’ in ‘constrained optimisation’ comes from; you can’t consume as much as you want because you are limited by your resources and so you aim to select the bundle of goods or activities that optimises your utility (happiness/ pleasure). The second important assumption is that the utility you get from any one good or activity doesn’t have a linear relationship with the amount of the good, ie your fourth slice of pizza isn’t as enjoyable as your first slice. This is known as diminishing marginal utility.
When considering how two goods are traded off against each other, economists use a ‘Cobb-Douglas’ function to create indifference curves. The Cobb-Douglas function states that utility (U) is equal to the amount of the first good, y (raised to a power), times the amount of a second good, x (also raised to a power). The rule is that the sum of the powers has to equal 1; ie if y was raised to the power of 0.5, then x would need to be raised to the power of 0.5, as in the equation below.
This utility function can be rearranged to show relationship between the quantities of x and y you need for a particular level of utility.
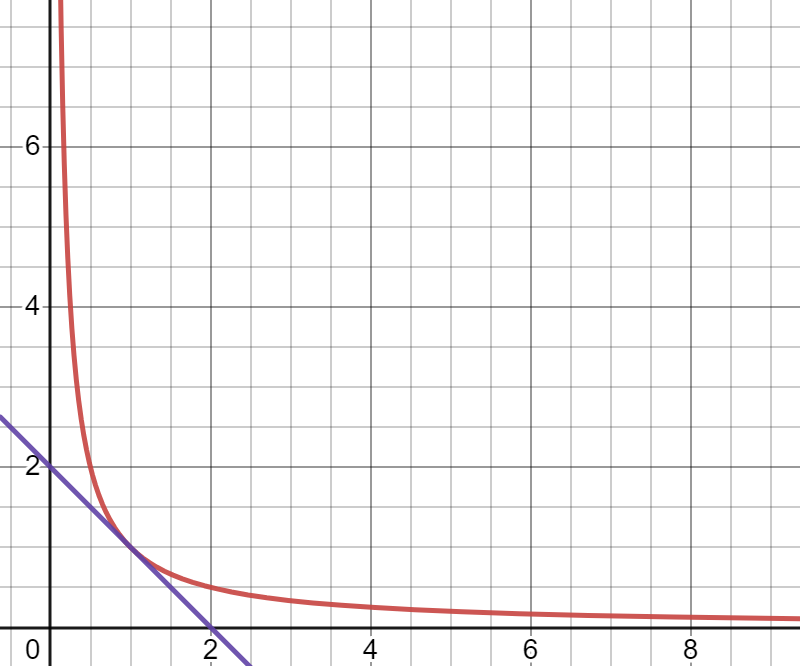
Graphically, this translates into ‘indifference curves’, as illustrated below. Each line (red, blue and green) represents combinations of x and y that produce the same utility, ie you are indifferent between the combinations that sit on each line.
Figure 1: Indifference curves
Where U2 = 1 (red line):
Where U2= 2 (blue line):
Where U2 = 3 (green line):
The curves are convex because you need a smaller total amount of goods to achieve the same utility when you have the same number of x and y. In other words, two apples and two bananas might give you as much utility as five apples and one banana, which is the consequence of diminishing marginal utilities. The shape of the curve is always convex because the powers that x and y are raised to must add up to no more than 1.
The second element that is needed for constrained optimisation is the constraint, which is conceptualised as a ‘budget’ line. Here you have a certain amount of money (K), and that is used up by buying a quantity of y at price p1 and a quantity of x at a price of p2. These are expressed as ‘prices’ but could equally be the amount of time taken to do y and the amount of time taken to do x and your ‘budget’ is the total amount of time you have. As with the Cobb-Douglas function, the equation can be rearranged to show the relationship between y and x for a specific budget, as shown below.
Plotted on a graph, these produce straight lines that move away from the origin (where the axis intersect) as the budget (K) increases, as shown on the graph below.
Figure 2: Budget lines
Where K = 2, p1 = 1, p2 =1 (purple line):
Where K = 2.8, p1 = 1, p2 =1 (black line):
Where K = 3.45, p1 = 1, p2 =1 (red line):
The final step is to combine figures 1 and 2 into as single graph, as shown below (with just one indifference curve and one budget line)
Figure 3: Constrained optimisation
The point where the budget line and the indifference curve just meet is the point of ‘constrained optimisation’, ie the combination of goods that produces the highest utility given the budget available.
This model is built on relatively simple concepts but results in an utterly profound insight into behaviour. When you reflect on it, you realise that almost every single one of the thousands of decisions we make everyday is the result of a constrained optimisation process. From the largest decisions about our choice of partner or our job or where we live to tiny ones about what kind of coffee we’re going to buy or how we’re going to travel somewhere. All these decisions involve choices and all are constrained in some way or other.
This framework also allows for a very clear analysis of the difference between interventions that aim to work through affecting choices (such as taxes and subsidies) and those that aim to work through affecting motivation or preferences (such as many health campaigns).
Choice interventions
1 – Changing people’s total budget
One ‘choice’ intervention could be increasing or decreasing people’s budget, for example through increasing or decreasing general tax or increasing benefits. Taking the positive example, increasing benefits will mean that in figure 4 below someone’s budget line will progressively move outwards from the purple one to the black one to the red one, each time moving up indifference curves and so increasing happiness and increasing the amount of both x and y but keeping the proportion of each the same.
Figure 4: Changing the budget
2 – Subsidising a particular behaviour
An alternative to just increasing or decreasing people’s overall budget is to change the relative prices of goods, for example by subsidising one. This will do two things. It will change the angle of the budget line but also mean that when you buy a combination of goods, you will increase the total number of goods you’re able to afford. To illustrate, if x now costs 0.5 rather than 1, the budget line becomes:
In figure 5, the original budget line is the purple one and the blue budget line is the new budget line. In this case, the solution to the constrained optimisation problem changes from the intersection with the red indifference curve to the intersection with the blue indifference curve. The result in an increase in utility, an increase in the amount of both goods consumed, and a greater proportion of good x compared to good y being consumed.
Figure 5: Subsidising x
One implication of this is that if you tax harmful goods, such as alcohol and tobacco, in the short term it will make people less happy (though in the long term it would be expected to increase their utility as they reap the health benefits). Addiction complicates this analysis, however, as people have more complex motivations, which means they may welcome additional restrictions despite it potentially reducing their immediate utility. A vivid example of this was the introduction of the indoor smoking ban in the UK in 2007, which was supported by a 78% of smokers[1] despite the fact that it would make their lives more difficult.
Motivation interventions
In contrast to choice interventions, motivation interventions aim to change people’s preferences. Coke’s yearly marketing budget is estimated to be $4bn, which is aimed at increasing people’s motivation or preference for the product, primarily through associating it with an aspirational lifestyle (rather than any characteristic of the sugary drink itself). Similarly, many health interventions aim to decrease people’s motivation or preferences for harmful products (such as sugary drinks, alcohol or tobacco), often by emphasising their negative qualities or by associating them with negative lifestyles. Within the constrained optimisation framework this can be represented as changing the powers that x and y are raised to within the Cobb-Douglas function. For example, an increase in the relative motivation for x might mean increasing the power it is raised to from 0.5 to 0.75, which would also mean decreasing the power y is raised to from 0.5 to 0.25, changing the equation for the indifference curve.
The result of this is that for a given level of utility, the indifference curves changes shape and shift ‘downwards’ in figure 6, from the red one to the blue one. However, the budget line now intersects the indifference curve, which means there is another indifference curve that just touches the budget line, which is shown in green.
Figure 6: Increasing relative motivation for x
Red indifference curve:
Blue indifference curve:
Green indifference curve:
The result of changing preferences in this way is that there is an increase in the amount of x consumed and a decrease in the amount of y that is consumed but that also total utility is increased, as the total utility is the fourth root of 1.7, which is 1.14, which is greater than 1.
This analysis illustrates that the effect on someone’s short term happiness of an intervention that changes their motivation will depend on the original balance of their preferences and on the relative cost of the goods. In this case, making someone’s preferences less balanced, increases their happiness. So if someone started off with a greater preference for sitting at home and watching TV than going to the gym and an intervention increased their preference for going to the gym, in the short term this could decrease their happiness (though in the longer term it may have the opposite effect as they become healthier). However, if the budget line was tilted anticlockwise (ie the price of going to the gym was made cheaper), then the budget line could just touch the blue indifference curve that was higher than the green one and so someone’s happiness wouldn’t be reduced in the short term. Intuitively this makes sense; if you increase someone’s preference or motivation for something that is relatively expensive, it is likely to make them less happy, whereas if you increase their motivation to do something that is relatively cheap, then it is likely to make them happier overall.
Conclusion
Using constrained optimisation as a framework helps clarify the difference between interventions that aim to change motivations and those that aim to change choices, as they are represented by distinct elements of the utility function and budget line. However, in addition this approach makes predictions that may be surprising to developers of interventions and policy makers, which is that something that changes people’s motivation can make them less happy even if the change is in favour of a ‘positive’ or health activity (at least in the short term). This might provide an additional explanation for why interventions such as weight loss programmes have limited success. If they decrease your happiness in the short term and the benefits don’t appear for some time, then your motivation may be undermined and you end up going back to eating unhealthily. This analysis also emphasises a crucial lesson of the integrated model, which is that it is important to consider the whole behavioural pathway when designing interventions. In the case of weight loss, the implication is that the most effective intervention will include motivational elements (to increase people’s preferences for eating healthily) and choice elements (to reduce the relative cost of eating healthily), resulting in changed behaviour and increased short term happiness as well as hopefully increasing health and happiness in the long term. This is something that each approach on its own will struggle to achieve.
[1] https://www.centreforpublicimpact.org/case-study/smoking-ban-united-kingdom